Pairs Trading
Pairs trading is a non-directional trading strategy that involves matching a long position with a short position in two stocks with a high correlation. This technique is widely practiced by hedge funds and institutional investors as a long/short equity investment strategy. While its relevance has been constantly tested with updated approaches, its profitability is acknowledged among practitioners and academics.
Currently, the co-integration method and the distance method are the most popular techniques used in pairs trading to identify the dependency structure. However, these two methods have some drawbacks, as they rely on assumptions that are not always met.
Specifically, both of these methods assume the divergence between the spread to be symmetrically distributed about the mean. If the two correlated stocks follow the joint normal distribution, the distribution of the spread in both distance method and cointegration method would be robust, while the spread itself can fully capture the dependency structure of the two stocks.
However, negative skewness and/or excess kurtosis are frequently observed in most financial assets.
The study of Okimoto (2014) finds strong evidence of the asymmetry dependency structure within the equity markets over the last 35 years, particularly the asymmetry of upper and lower tail dependence structure.
Hence, employing traditional distance and cointegration methods in modeling joint behavior, as done in the majority of quantitative methods to date, would poorly represent the actual relationship among the assets.
This leads to the evocation of a new method, Copulas. The application of copulas would be beneficial in relaxing the symmetry restriction that correlation and cointegration enforce on the pairs’ dependence structure.
Copulas are useful extensions and generalizations of approaches for modeling joint distributions and dependence between financial assets.
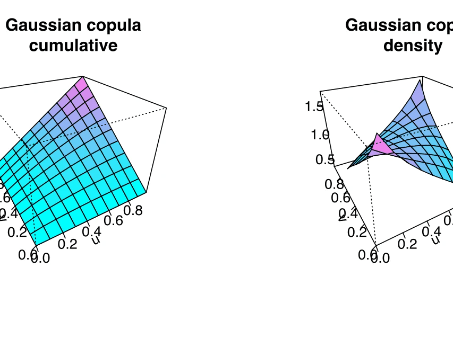
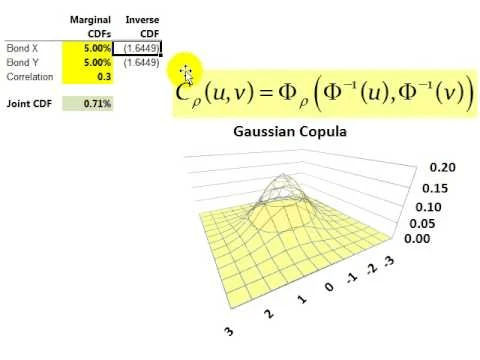
A copula is a function that links marginal distribution functions to their joint distribution function. A copula captures the dependence structure between the marginal distributions so that it can be applied regardless of the marginal distributions’ form.
Unlike the conventional approaches, employing a copula-based approach results in a far richer set of information, such as the shape and nature of the dependency between the stock pairs, instead of restricting the framework towards the elliptical dependence structure.
This advantage results from the variety of choices of copulas including Gaussian, Student-t, Archimedean copulas (Clayton, Frank, Gumbel), etc. For example, the Clayton copula captures lower tail dependence, the Frank copula is suitable for modeling data characterized by weak tail dependence, and the Gumbel copula captures both strong upper tail dependence and weak lower tail dependence.
In the following plot from Liew et al. (2013), we can see the Gumbel copula matches the dependence structure, especially the density at the extreme ends, which makes more sense compared with the normal elliptical copula. Therefore, it would potentially lead to a superior pairs trading strategy by allowing for more flexibility in capturing asymmetries in the dependence structure within pairs.
The empirical results also suggest that the copula-based pairs trading strategy is a potentially powerful analytical alternative to the traditional techniques. Both Rad et al. (2016) and Liew et al. (2013) showed that the distance and cointegration method strategies suffer from a decline in trading opportunities.
In contrast, the copula method remains stable in presenting such opportunities, as it does not require any rigid assumptions. Krauss et al. (2017) developed a copula-based pairs trading framework and applied it to the S&P 100 index constituents from 1990 to 2014, which shows low volatility, leading to annualized Sharpe ratios of 1.52.
Nevertheless, more elaborate models can also result in inferior performance, especially out of sample, by introducing issues such as over-fitting. Moreover, the computational requirements necessary to process these mathematically complex algorithms may outweigh their relative performance improvements over simpler strategies. This might result in the weakening of motivation to adopt such strategies in practice.
In short, the currency pair trading strategy is still profitable and remains strong under highly volatile market conditions. The trading opportunity for strategies based on distance and cointegration is declining in recent years, while the copula-based strategy has been stable. In this regard, the copula method is promising and deserves further attention from practitioners and academia.
Written by Wo Zhang
Edited by Kevin Ma, Thomas Braun, Alexandar Ristic, Bryan Xiao, Jack Argiro, Junping Chen & Alexander Fleiss
Mahfoud, M., and M. Michael. "Bivariate Archimedean copulas: an application to two stock market indices." BMI Paper 1517333 (2012). https://beta.vu.nl/nl/Images/werkstuk-mahfoud_tcm235-277460.pdf
Liew, Rong Qi, and Yuan Wu. "Pairs trading: A copula approach." Journal of Derivatives & Hedge Funds 19.1 (2013): 12-30. https://link.springer.com/article/10.1057/jdhf.2013.1
Okimoto, Tatsuyoshi. "Asymmetric increasing trends in dependence in international equity markets." Journal of Banking & Finance 46 (2014): 219-232. https://www.sciencedirect.com/science/article/pii/S0378426614001927?casa_token=gUJ9Qi6qg7gAAAAA:0q-UA1ZsbxcxszrjDW3Cl9mW7KrwikDGkNj6b7t1-lKRzOklmt4QwgKKZRgl23gW8tCSfw
Rad, Hossein, Rand Kwong Yew Low, and Robert Faff. "The profitability of pairs trading strategies: distance, cointegration and copula methods." Quantitative Finance 16.10 (2016): 1541-1558. https://doi.org/10.1080/14697688.2016.1164337
Krauss, Christopher. "Statistical arbitrage pairs trading strategies: Review and outlook." Journal of Economic Surveys31.2 (2017): 513-545. https://doi.org/10.1111/joes.12153
Krauss, Christopher, and Johannes Stübinger. "Non-linear dependence modelling with bivariate copulas: Statistical arbitrage pairs trading on the S&P 100." Applied Economics49.52 (2017): 5352-5369. https://doi.org/10.1080/00036846.2017.1305097